INTRODUCTION

A while ago I started messing around with the ncurses library, which is used to build text-based user interfaces fo the command line on Linux/Unix systems. In short, it is used to manipulate the characters displayed by the shell and allows for the creation of a more pleasing graphical front-end for terminal applications. At the time I was reading Stephen Wolfram’s (free) book “A New Kind of Science“, in which he gives an introduction to the fascinating cellular automata. “Rule 30” aka. the elementary cellular automaton might be the most prominent example of such a thing and it is often used as an example for a chaotic system deterministically based on very simple rules.

Another famous example is the amazing John Conway’s “Game of Life“. I recommend watching some youtube videos on the topic after you finish reading this post. It is a huge rabbit hole if you are into these kind of things..! Here is a fantastic video that absolutely amazed me the first time I saw it:

Alan Zucconi: Let’s BUILD a COMPUTER in CONWAY’s GAME of LIFE

(Don’t be put off by the title. No real computers are built in the video, and it’s definitely worth watching without a background in computer science!)

So far so good, let’s look into how the classic elementary cellular automaton works.

THE RULES

An elementary cellular automaton is a state machine based on cells, that can either be dead or alive (black and white or 1 and 0 also work for that matter). In the case of Wolfram’s Rule 30 the state is single a row of cells, so it is 1-dimensional. The automaton then iterates over the cells in the current state to find its next state by applying a special rule set. This newly found state in turn becomes the current state and so on. If we plot the sequence of states as lines below each other, we arrive at images like shown in the examples here.

Let’s have a closer look at how the rules work. In this example we will see how rule number 30 actually works. Only one prerequisite exists – you have to understand counting in binary. To determine the status of any given cell in the next iteration, we have to look at its neighborhood, i.e. the cell itself with its two adjacent cells. If we express this in terms of 1s and 0s, we thus arrive at 3-bit binary numbers, which can hold any value in the range of 0-7. Now all that’s left is to define a set of rules, or simply a rule, which tell us whether the cell is alive or dead in the next step based on its current neighborhood. More precisely, for each of the eight possible neighborhoods we can decide whether a cell dies or or survives another round. Here’s a visualization of the process:

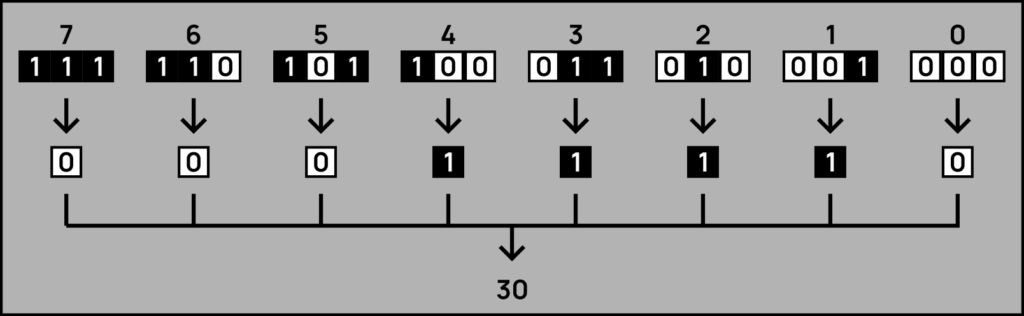
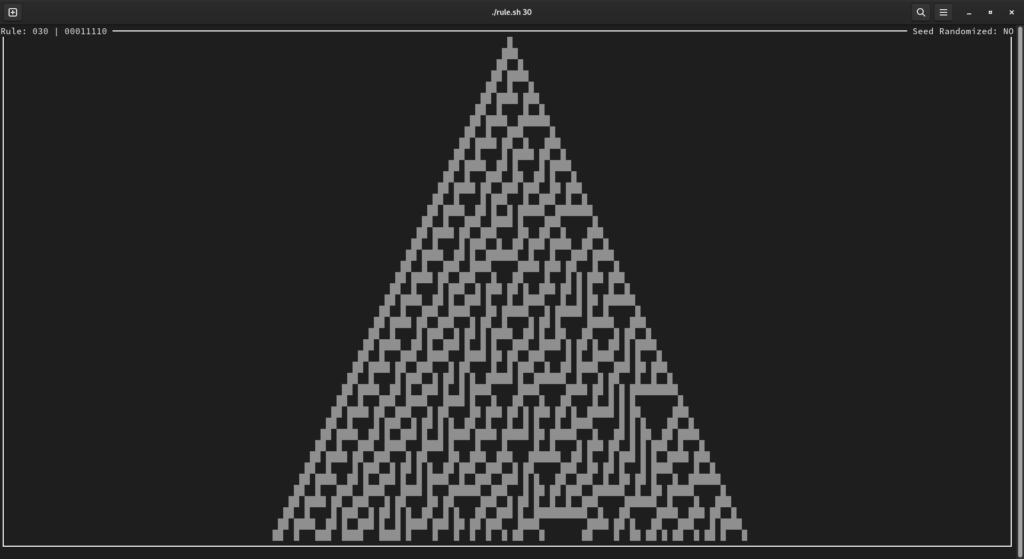
As we can see, the number 30 (00011110 in binary) is just the decimal representations of one of the possibilities of how a cell behaves next turn depending on its neighborhood. In total there are eight rule bits, which makes 256 different possible rules (0-255). Both rules on the extreme ends are rather boring. The 0 rule just kills all cells no matter what and the 255 rule simply sets all cells alive, so they result in all white/black cells after one interation respectively. But this is obviously not the case for other rules! Some of them show very regular behaviour and can even result in fractal patterns like in the example shown below.

Other rules like the infamous rule 30 show chaotic behaviour instead. They never start repeating and have no recognizable “pattern” (at least not one that goes on forever). Chaos is emerging from a set of rules that can be encoded in 8 bits.

There are even situations in which these patterns naturally occur, e.g. on seashells or the skin patterns on some lizards to name a few. In the case of rule 110 it has been shown that it is capable of universal computation, meaning it is Turing complete!
(Don’t worry if you do not understand this yet. The video linked above does a great job at explaining what Turing completeness is using Conway’s game of life.)

THE NCURSES AUTOMATON

With my own implementation it is possible to step through the iterations, animate the process and even randomize rules while running the automaton. It works quite well to play around and get a feel for what the elementary automata can do. (See some more screeshots below.)

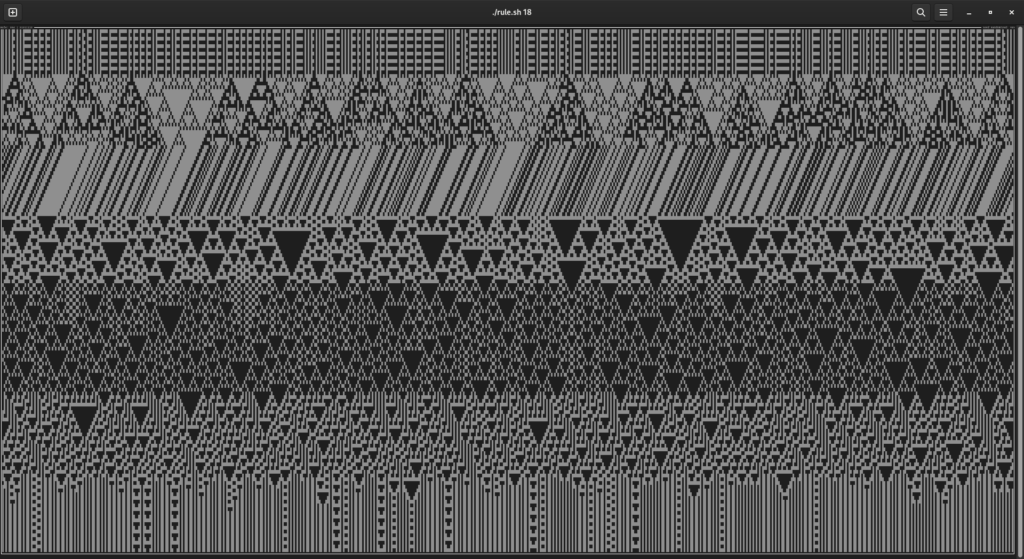
The project can be found on GitHub if you want to try it for yourself. I have explained how to use the ncurses-Cellular-Automaton in greater detail over there and the repository also hold more output images that show the fractal patterns that can emerge.

The whole idea of cellular automata is a huge topic and has many interesting facettes. Try skipping through Wolfram’s book or watch Zucconi’s video for more examples of different automata. In more complex cases like the Lenia project the results can seem strikingly “alive”. It is absolutely intriguing how far the rabbit hole goes, and how little we actually understand about the fundamentals of these machines.